Supplementary webpage for the paper "A Formal Evaluation of DepDegree Based on Weyuker’s Properties"
You can download the paper from here.
Complexity of source code is an important characteristic that software
engineers aim to quantify using static software measurement. Several
measures used in practice as indicators for software complexity have
theoretical flaws. In order to assess the quality of a software measure,
Weyuker established a set of properties that an indicator for program-code
complexity should satisfy. It is known that several well-established
complexity indicators do not fulfill Weyuker’s properties. We show
that DepDegree, a measure for data-flow dependencies, satisfies all of
Weyuker’s properties.
This webpage contains an introduction of the programming language used in the
proofs (Sec. 1) and an explanation of DepDegree (Sec. 2).
Appendix 1: Language used in proofs
We use an artificial language, first described by Weyuker [5]. We use this language
because it has a simple syntax, which makes it convenient for such formal
evaluations, while still exposing the same theoretical expressive power as popular
programming languages (Turing completeness).
The language consists of programs, which are composed of a program statement
(progstmt),
a body,
and an output statement (outstmt).
Program and output statements both have variables (vars), which are the input and output variables,
respectively. A program body can be an assignment (asgn), a conditional expression,
a loop, or a composition of two program bodies. An assignment sets a value, which
is given by an expression, to a variable (var).
An expression is either one value or an arithmetic operation (arop) applied to two values.
A value may either be a constant (const) —a number— or a variable (var).
We require all variables to be defined prior to their use in an expression.
Instead of using a semicolon character, the two program bodies of a composition can also be
distinguished by a newline character.
Conditional statements and loops require predicates, which are two values composed using a comparative operator
(compop).
For a given measure m and a given program P, we denote the measurement
result m(P) by |P| if the measure m is clear from the context. Even though some of
the properties are defined in reference to program bodies, we assume a definition
of every variable prior to its use. In the program fragments that we use
in this paper, definitions that are missing in a program body are assumed
to be defined in a previous program statement that is not printed in the
figure.
To express that the functionality of two programs P and Q is identical, we write
P ≡ Q. This means that (1) the sets of variables of the program statement and the
output statement are identical in P and Q, (2) for a given configuration of input
variables, the values of the output variables are identical in P and Q, and
(3) program P halts if and only if Q halts.
Appendix 2: DepDegree
Intuitively, in the data-flow graph of the program, each program operation op has an
edge back to each program operation that assigned a value to a variable used in op.
The DepDegree of a program operation is the sum of such edges, over all variables
and all back edges to definitions for each variable. The DepDegree of a program is the
sum of the DepDegrees of all program operations (or shorter: the total number of
edges in the data-flow graph of the program).
Formally, we base the definition of DepDegree on a program represented
by a control-flow graph G = (B,f). The graph G is a directed graph with
the set F ⊆ B × B of edges representing the control-flow between program
operations B [1]. In our language (Fig. 1), a program operation can be an
assignment operation with one exit edge or a conditional with two exit edges. We
denote the set of program variables by X.
The definition of operation dependency is derived from the notion of reaching
definitions, a well-known concept in compiler design and data-flow analysis. The
function reaching definition rdG = B ×X → 2B for a control-flow graph G assigns to
a program operation b and a variable x a set of all program operations that define the
variable x prior to b and are reaching definitions. That means there must exist a path
in G from br ∈ B to b, such that br defines x and no program operation on the path
from br to b redefines x.
A use-def graph SG = (B,E) for a control-flow graph G is a directed graph with
the set of program operations B and the set E ⊆ B × B of use-def edges. There
exists a use-def edge e = (bv,bu) for two program operations bv and bu if there is a
variable x that is used in bv for which rdG(bv,x) holds.
So, for every edge in the use-def graph we know that there is a data-flow
dependency between the program operations bv and bu, where the former is using a
variable definition made in the latter. We call this graph the dependency
graph.
The DepDegree of a program operation b is the number of program operations
that it depends on. Formally, the DepDegree of a program operation is a function
ddG : B → ℕ that assigns to each program operation b the number of outgoing edges
of b in the use-def graph SG, such that dd(G) = 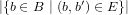 . The
DepDegree of a control-flow graph G = (B,F) is defined as the function dd : G → ℕ
that assigns to a CFG G the number of edges in its dependency graph S = (G,E).
Formally, dd(G) = ∑
b∈BddG(b) = |E|. For a method w, we use dd(w) = dd(G),
where Gis w’s CFG.
. The
DepDegree of a control-flow graph G = (B,F) is defined as the function dd : G → ℕ
that assigns to a CFG G the number of edges in its dependency graph S = (G,E).
Formally, dd(G) = ∑
b∈BddG(b) = |E|. For a method w, we use dd(w) = dd(G),
where Gis w’s CFG.
DepDegree is a relatively new measure, but the results of its first evaluation and
comparison to long-established measures are promising [4, 2].
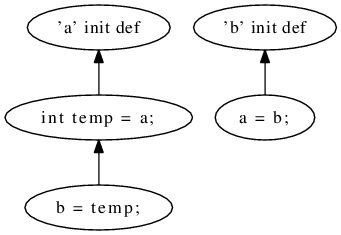
Example. Figure 2 shows two alternative implementations of a method for swapping
variable values. The first exploits arithmetic properties of integers, the second uses a
temporary variable to store the value that would otherwise be overwritten.
Apparently the two implementations are different in their complexity of the program
code: one is more difficult to understand than the other. DepDegree offers an
explanation for this: Consider the respective use-def graphs in Fig. 3, in which the
first implementation has 6 edges and therefore a measurement value for DepDegree of
6, while the second only has 3 edges and thus a measurement value of 3. In this
example, DepDegree is sensitive to the different complexity of program code, and
confirms the opinion of many developers that the first method is more difficult
to understand than the second. (For comparison, the measure statement
count yields the value 3 in both cases, and the cyclomatic complexity is 1 for
both.)
References
[1] A. V. Aho, R. Sethi, and J. D. Ullman. Compilers: Principles,
Techniques, and Tools. Addison-Wesley, 1986.
[2] D. Beyer and A. Fararooy. DepDigger: A tool for detecting complex
low-level dependencies. In Proc. ICPC, pages 40–41. IEEE, 2010.
[3] D. Beyer and A. Fararooy. A simple and effective measure for complex
low-level dependencies. In Proc. ICPC, pages 80–83. IEEE, 2010.
[4] B. Katzmarski and R. Koschke. Program complexity metrics and
programmer opinions. In Proc. ICPC, pages 17–26. IEEE, 2012.
[5] E. J. Weyuker. Evaluating software complexity measures. IEEE
Trans. Softw. Eng., 14(9):1357–1365, 1988.
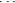 | ‘z’
| ‘z’  | ‘9’
| ‘9’ 
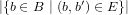 . The
DepDegree of a control-flow graph
. The
DepDegree of a control-flow graph